Deep Reinforcement Learning to Beat Blackjack

Beating Blackjack with Deep Reinforcement Learning

I was on vacation with friends and we were playing blackjack a lot. Of these, two are Physicists, one Management Engineer (the dealer and most expert player), and me, the Computer Scientist. We decided to count the win/lose ratio. Then, I opened a Colab Notebook. Starting with some Monte Carlo Simulations, I decided to use Reinforcement Learning to let the model choose the perfect action.

Why Reinforcement Learning? It's the leading Machine Learning class to beat humans in games (see Google DeepMind AlphaGo and beyond!). And I'm on vacation! I don't want to think of an optimal strategy, let the RL model decide the perfect action!

…and during my free time in a couple of days, I published this article. Using libraries like gymnasium for the environment and stable-baselines3 for the A2C and PPO agents and policies, I try to beat Blackjack with Reinforcement Learning.

Note: this is just an experiment made in a couple of days just for fun. I may improve it with new features in the future. Meanwhile, use it at your own risk.

Full code: Colab Notebook

This article is on Medium!

The Game

Blackjack is a card game where the goal is to beat the dealer by obtaining cards that sum to closer to 21 (without going over 21) than the dealers cards.

To represent the table I use a dict(): the keys are the player_id and the values the list of cards in their hand. The dealer has id -1.

An example of a game: Player 0 loses against the dealer (-1).

start game: {0: ['9', '3'], -1: ['3', '8']}
next turn: 0 step: {0: ['9', '3', '7'], -1: ['3', '8']}
next turn: -1 step: {0: ['9', '3', '7'], -1: ['3', '8']}
next turn: -1 step: {0: ['9', '3', '7'], -1: ['3', '8', '3']}
next turn: -1 step: {0: ['9', '3', '7'], -1: ['3', '8', '3', '7']}
result: [-1]

Monte Carlo Simulation

The Monte Carlo simulation is a mathematical technique that predicts possible outcomes of an uncertain event. Computer programs use this method to analyze past data and predict a range of future outcomes based on a choice of action.

Let's use this Monte Carlo simulation for a simple Blackjack strategy: if the value of my hand is below 17 I take a card, else I stay. Using Monte Carlo with 100 iterations for 1000 games.

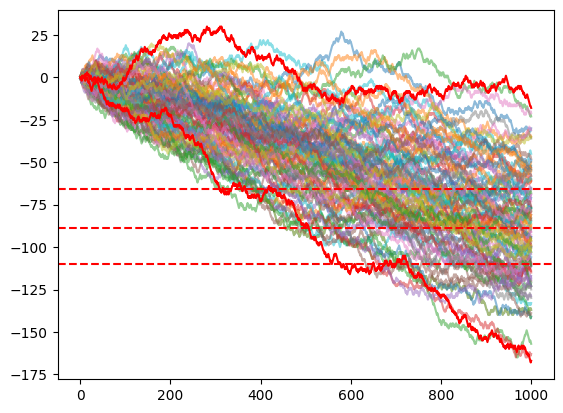
Deep Reinforcement Learning

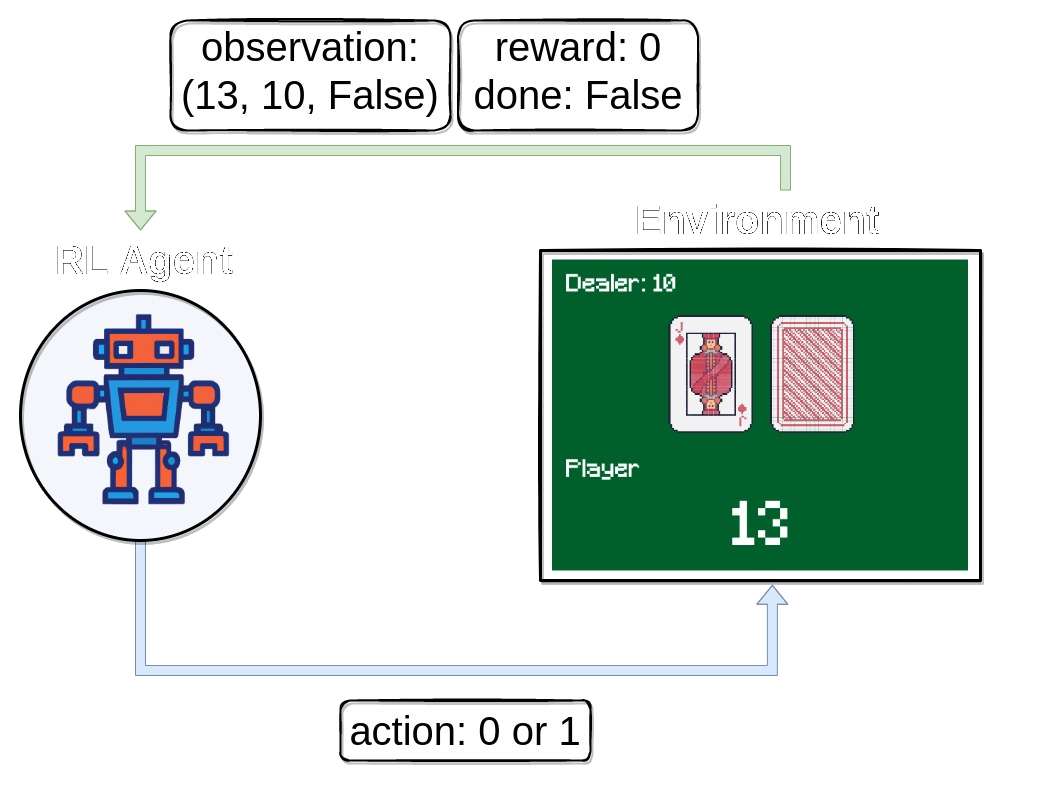
Reinforcement Learning is an area of machine learning concerned with how intelligent agents ought to take actions in an environment in order to maximize the notion of cumulative reward.

To use Reinforcement Learning to beat the dealer in blackjack I have to define:

• Action Space: of the player (agent)
• Observation Space: which data should the model use to make a decision for the action?
• Reward: to improve the model

The libraries I used for the Reinforcement Learning are stable-baselines3 for the agents and the policies, and gymnasium for the environment.

Action Space

The action shape is (1,) in the range 1 indicating whether to take a card or stay.

• 0: Take Card
• 1: Stay

Observation Space

The observation shape is a Box of shape (1, 39) containing:

# observation space
self.observation_space = Box(low=-np.inf,high=np.inf, shape=(1,len(self.deck.CARDS)*3))

# observation
def __next_obs(self):
      obs = self.__hand_to_count(self.bj.get_hand(0))+self.__hand_to_count(self.bj.get_dealer_hand())+[v for v in self.deck.counter.values()]
      return (np.array(obs)/self.deck.n_deck).reshape(1, len(obs))

The observation is the sum of 3 lists: my hand list count, dealer hand list count, and deck cards count. The list is length 13 to represent the count of all cards. Some examples:

my_hand = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1] # A = 1, K = 1
6_decks = [24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24] # init count of 6 decks

This means that to beat the market I'm giving the model the possibility to count the carts of the deck to make a decision. From this data, the model will create its own strategy.

Rewards

• win game: +1
• lose game: -1
• draw game: 0

Train

To train on the environment defined I use the library stable-baselines3 for the agents and the policies. I decided to use and compare two agents:

• A2C: A synchronous, deterministic variant of Asynchronous Advantage Actor Critic (A3C).
• PPO: The Proximal Policy Optimization algorithm combines ideas from A2C (having multiple workers) and TRPO (it uses a trust region to improve the actor).

Note: below I trained and tested the models with 2 decks. I tried also with 6 or more and it still reaches the same results after thousands of more games of training.

env = EnvBlackJack(Deck(2))

for agent in ['PPO','A2C']:
  for policy in ["MlpPolicy"]::
    print(agent,policy)
    agents = {'PPO':PPO,'A2C':A2C}
    model = agents[agent](policy, env, verbose=1)
    model.learn(total_timesteps=20_000, progress_bar=True)
    model.save(f"{agent}_{policy}")
    del model

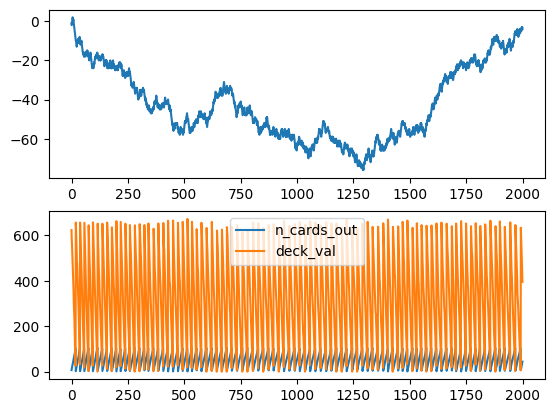
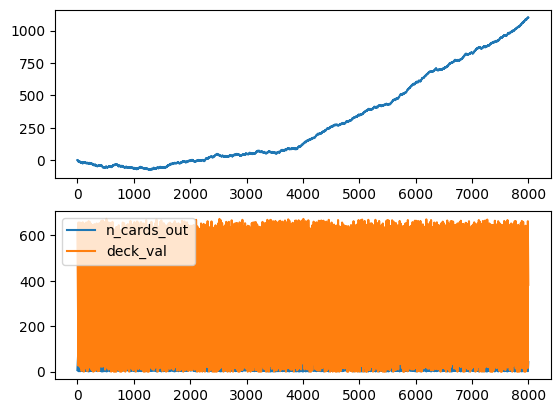
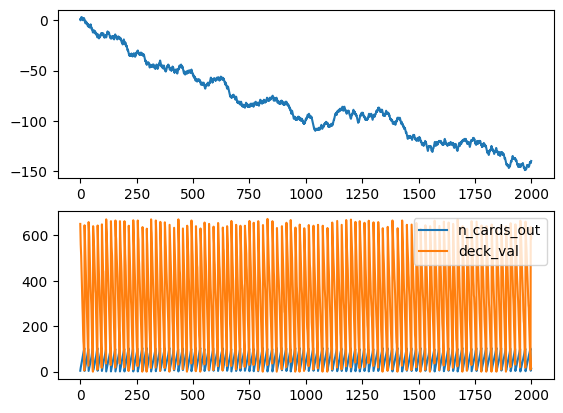
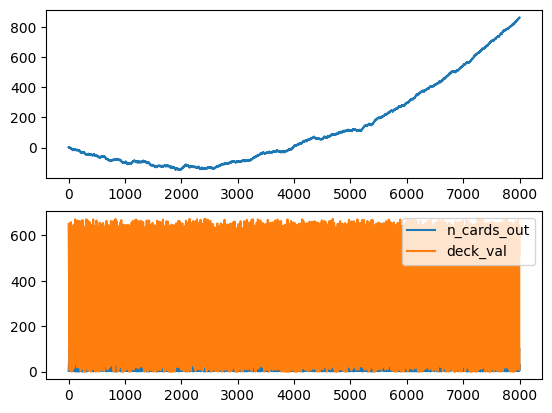
The A2C starts to improve after around 1300 games while the PPO after 2000, and the cumulative sum of rewards and win/lose/draw reach impressive highs.

Test models

To test the trained models, I use the Monte Carlo Simulation with the action predicted by the models. As the initial test, I use 100 iterations for 1000 games.

for agent in ['PPO','A2C']:
  for policy in ["MlpPolicy"]:#,"CnnPolicy"]:
    print(agent,policy)
    agents = {'PPO':PPO,'A2C':A2C}
    loaded_model = agents[agent].load(f"{agent}_{policy}")
    env = EnvBlackJack(Deck(6), vis=VisualizerMonteCarlo, verbose=False)
    obs, _ = env.reset()
    while not env.vis.is_done:
        action, _states = loaded_model.predict(obs)
        obs, rewards, done, _, _ = env.step(action)

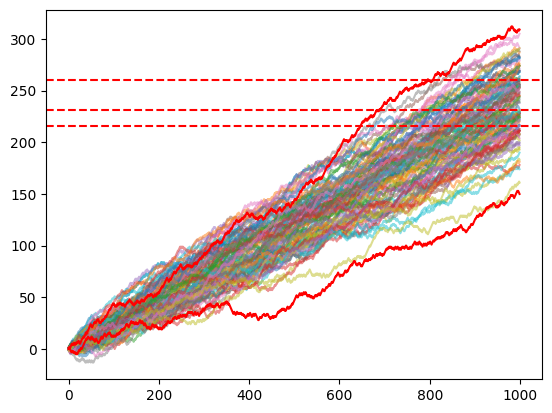
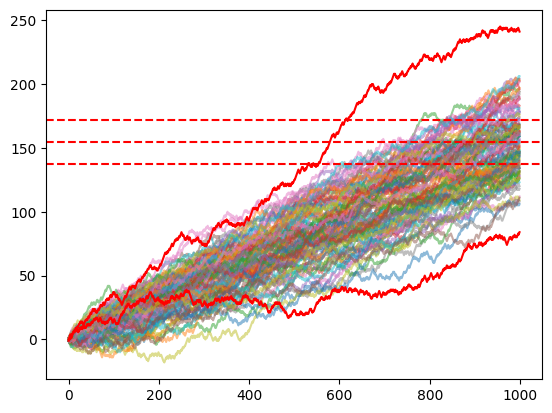
Conclusions

Surprisingly, both models seem to beat the dealer. How is that possible? First of all, we have to consider that both the train and the test were made with just 2 decks. Even though I tried with 6 and more, it still reaches good results but needs additional training time. In addition, as written at the beginning of this article, this is just an experiment I made in my free time for a couple of days during vacations with my friends. I probably made some errors, but it led to interesting results and thoughts about the power of Reinforcement Learning in card games and in general.

This experiment could be definitely improved: performance comparison with several decks, more actions of the game (split, …), and most important understanding the decision of the model with some plots and data.

References

https://gymnasium.farama.org/tutorials/training_agents/blackjack_tutorial/

https://stable-baselines3.readthedocs.io/en/master/guide/algos.html